Calculating areas and volumes

calculus

Lecture 6.1 - Area Calculations with Integrals - Vertical Strips (dx) vs. Horizontal Strips (dy) (Links to an external site.)

• DONE Completed: 2022-05-04 https://youtu.be/ssB9UiXUDKg

We could use dy instead of dx for area under the curve.

Example: area enclosed by: $f(x)=x$ and $g(x)=\sqrt{x}$.

@axis
f(x) = x
g(x) = x**.5
plot f(x),g(x)

instead of f(x) and g(x), just put y.

$y=x\text{ and }y=\sqrt{x}$.

$\begin{array}{rl}x& =\sqrt{x}\\ x^2& =x\\ x^2-x& =0\\ x(x-1)& =0\\ [x=0,x=1]& \end{array}$

Things we know:

$\begin{array}{rl}{\int }_0^1& \sqrt{x}-xdx\\ & =\frac{2}{3}{x}^{\frac{3}{2}}-\frac{1}{2}{|}_0^1\\ & =(\frac{2}{3}-\frac{1}{2})-0\\ & =\frac{1}{6}\end{array}$

Different way:

$\begin{array}{rl}y& =x\text{ first one}\\ y& =x^2\text{ second}\\ y^2& =x\\ {\int }_0^1& y-y^{2}dy\\ & =\frac{1}{2}{y}^2-\frac{1}{3}{y}^3{|}_0^1\\ & =\frac{1}{2}-\frac{1}{3}-0\\ & =\frac{1}{6}\end{array}$

Example 2

@axis
f(x) = log(x)
h(x) = 2
 
plot f(x), 0 title "g(y)=0"
set arrow from 2, graph 0 to 3, graph 1 nohead

Technique is useful to simplify formulas sometimes. $\begin{array}{rl}{\int }_1^2\ln (x)dx& \\ u& =\ln (x)\\ du& =\frac{1}{x}dx\\ v& =x\\ dv& =dx\\ & =x\ln (x){|}_1^2-{\int }_1^{2}x\cdot \frac{1}{x}\\ & =2\ln (2)-\ln (1)-{\int }_1^{2}x\cdot \frac{1}{x}\\ & =2\ln (2)-1\end{array}$

^ Have to use integration by parts, which is a more advanced technique.

Alternatively:

$\begin{array}{rl}& {\int }_0^{\ln (2)}2-e^{y}dy\\ & =2y{e}^y{|}_0^{\ln (2)}\\ & =2\ln (2)-e^{\ln (2)}-(0-1)\\ & =2\ln (2)-1\end{array}$

Example 7.1.1 (book) $\begin{array}{rl}{\int }_0^{4\pi }& \sin (x)+2-(\frac{1}{2}\cos (2x)-1)\\ {\int }_0^{4\pi }& \sin (x)-{\int }_0^{4\pi }\frac{1}{2}\cos (2x)+{\int }_0^{4\pi }3\\ -cos(x){|}_0^{4\pi }-\frac{1}{2}{\int }_0^{4\pi }\cos (2x)+{\int }_0^{4\pi }3& \\ u=2x& \\ du=2dx& \\ -cos(x){|}_0^{4\pi }-{\int }_0^{8\pi }\frac{1}{4}\cos (u)du+{\int }_0^{4\pi }3& \\ -cos(x){|}_0^{4\pi }-\frac{1}{4}\sin (u){|}_0^{8\pi }+3x{|}_0^{4\pi }& \\ 0-0+12\pi & \end{array}$

Lecture 6.2 - More Horizontal vs. Vertical Area Integrals (Links to an external site.)

• DONE Completed: 2022-05-08 https://youtu.be/ndQdMkF3Gvs

Example

reset
@axis
f(x) = x**.5
g(x) = 2-x
h(x) = 0
plot f(x), g(x), h(x)

Find point of intersection. 0 & sqrt

sqrt and 2-x 2-x = sqrt(x) (2-x)^2 = x x^2-4x+4 = x x^2-5x+4 = 0 (x-4)(x-1) = 1 or 4

2-x and 0: 2

If we use DX, we have two problems. ${\int }_0^1\sqrt{x}-0dx+{\int }_1^2(2-x)-0dx$ $\begin{array}{rl}& {\int }_0^1\sqrt{x}-0dx+{\int }_1^2(2-x)-0dx\\ & =\frac{2}{3}{x}^{\frac{3}{2}}{|}_0^1+(2x-\frac{1}{2}{x}^2){|}_1^2\\ & =\frac{2}{3}-0+(4-2)-(2-\frac{1}{2})\\ & =\frac{2}{3}+2-\frac{3}{2}\\ & =\frac{2}{3}+\frac{1}{2}\\ & =\frac{4}{6}+\frac{3}{6}\\ & =\frac{7}{6}\end{array}$

For DY, it’s: ${\int }_0^1(2-y)-y^{2}dy$.

$\begin{array}{rl}& {\int }_0^1(2-y)-y^{2}dy\\ & =2-\frac{1}{2}{y}^2-\frac{1}{3}{y}^3{|}_0^1\\ & =2-\frac{1}{2}-\frac{1}{3}-0-0\\ & =\frac{7}{6}\end{array}$

Can we go over how we translate functions from their x counterparts to y? Especially y=sqrt(x) = y^2=x.

• DONE Completed: 2022-05-04

Try to get x on a side by itself. That gives you the answer.

Lecture 6.3 - Volumes of Rotation with Cross-Sectional Disks

• DONE Completed: 2022-05-08 https://youtu.be/i2mqBfdXuDQ

Find the solid obtained by parabola $y=1-x^2$ and the x-axis and rotating it about the y-axis.

@axis
f(x) = 1-x**2
plot f(x)

Gives a domed pyramid. It has circular cross-sections. The radius is 1/2 of the full width.

Volume of the cylinder is $\pi r^2\cdot h$

$\begin{array}{rl}& {\int }_0^1\pi (y-1)dy\\ & {\int }_0^1\pi y-\pi )dy\\ & =\pi y-\frac{\pi }{2}{y}^2{|}_0^1\\ & =\pi -\frac{\pi }{2}-0\\ & =\frac{\pi }{2}\end{array}$

Stack of washers (domed pyramid of donuts)

First quadrant is bounded by $y=e^x$, $y=1$ , and $x=1$ and rotated on the x-axis.

@axis
f(x) = exp(x)
plot f(x)

Empty interior is 2 wide, 1 tall. Going to do it DX so that they’re in the plane of the thing we’re trying to calculate.

Inner radius: 1 Outer radius: e^x Volume of thing: $\pi (e^x{)}^{2}dx-\pi dx$

$\begin{array}{r}{\int }_0^1\pi (e^{2x})-\pi dx\end{array}$

Q: Because we took the function y=1-x^2, why is the radius x=sqrt(1-y) and not x=1/2 sqrt(1-y) since we’re only dealing w/ half of it?

• DONE Completed: 2022-06-08

I don’t really understand how to differentiate things that involve the e constant.

• DONE Completed: 2022-05-11

u = 2x du = 2dx

limits change b/c u scales differently. $\begin{array}{rl}{\int }_0^1(\pi e^{2x}-\pi )dx& \\ u=2x& \\ du=2dx& \\ \frac{1}{2}{\int }_0^1(\pi e^{2x}-\pi )2dx& \\ \frac{1}{2}{\int }_0^2\pi e^u-\pi du& \\ & =\frac{1}{2}(\pi e^u-\pi u){|}_0^2\end{array}$

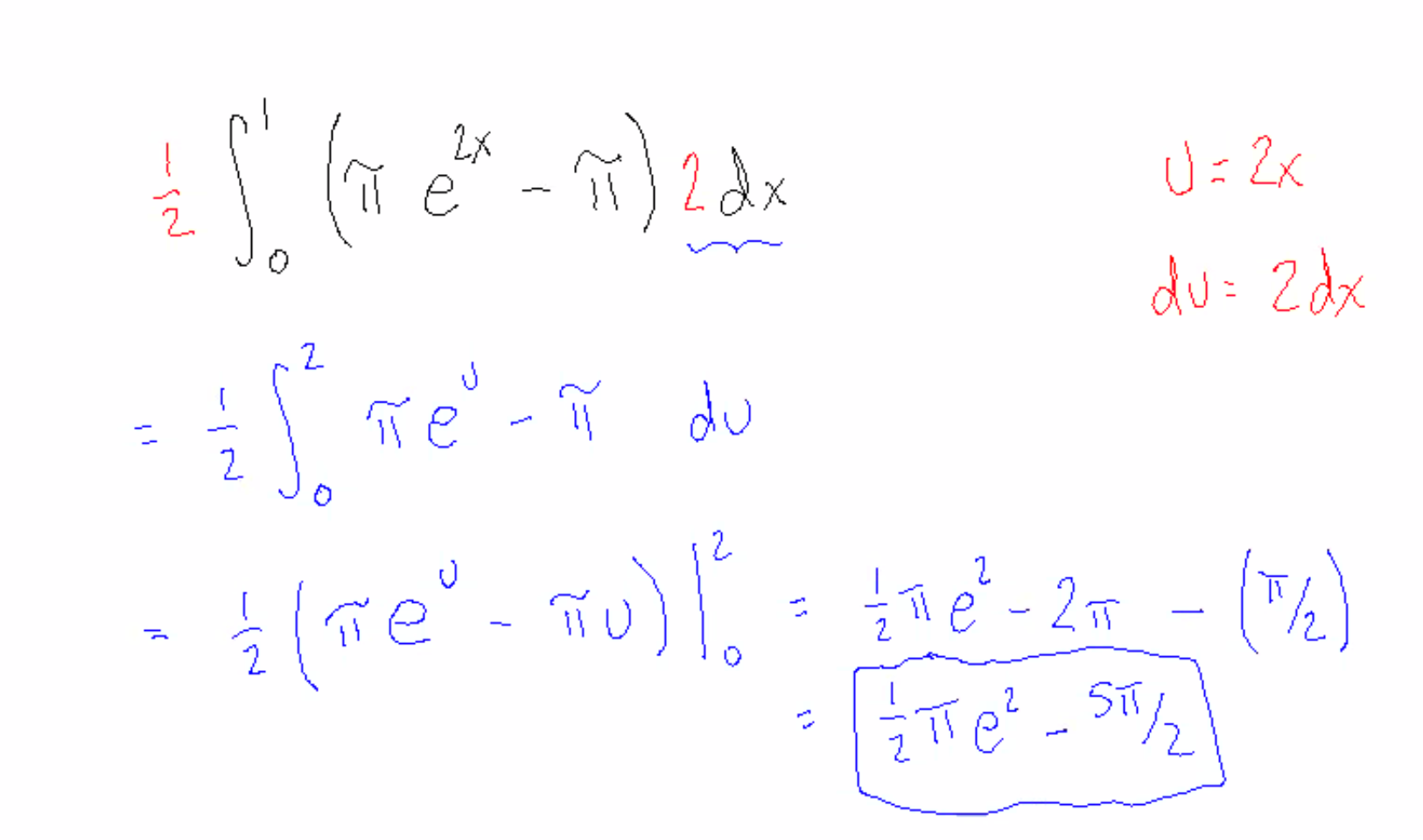
so e^{2x} differentiates into e^2x * derivative of 2x (so 2). (chain rule)

$\begin{array}{r}\int e^{2x}=2e^{2x}\end{array}$

The anti-differentiation of e^2x =1/2 e^2x (because the differentiation [2e^2x] would need to cancel out the 1/2)

Lecture 6.4 - A Geometric Formula from a Volume of Rotation

• DONE Completed: 2022-05-08 https://youtu.be/ptlVsJJt490

Basically, this is how to derive the formula for the volume of a sphere, but done via calculus.

Formula for a circle at 0,0 is $x^2+y^2=r^2$ (see geometry). In terms of x, that’s $x=\sqrt{r^2-y^2}$

$\begin{array}{rl}& {\int }_{-r}^r\pi (r^2-y^2)dy\\ & {\int }_{-r}^r\pi r^2-\pi y^{2}dy\\ & =\pi r^{2}y-\frac{\pi }{3}{y}^3{|}_{-r}^r\\ & =(\pi r^3-\frac{\pi }{3}{r}^3)-(-\pi r^3+\frac{\pi }{3}{r}^3)\\ & =2\pi r^3-\frac{2\pi }{3}{r}^3\\ & =\frac{4}{3}\pi r^3\end{array}$

Why isn’t this halved? I would guess that we do a 360 w/ the “rotate around” not, 180?

• DONE Completed: 2022-06-08

Lecture 6.5 - Integral Volumes Using Cylindrical Shells

• DONE Completed: 2022-05-09 https://youtu.be/aWs2SdczJxQ

Okay, so the “little slice” this time is a thin walled toilet paper roll, which is represented as $dr$.

$\begin{array}{rl}& =\pi (r+dr{)}^{2}h-\pi r^{2}h\\ & =\pi (r+dr)(r+dr)h-\pi r^{2}h\\ & =\pi h{r}^2+\pi h2r(dr)+\pi h(dr{)}^2-\pi r^{2}h\\ & =\pi h2r(dr)+\pi h(dr{)}^2\end{array}$

when $dr\approx 0$, it’s $\pi h2r(dr)$ … because $\pi h(dr{)}^2$ is “very small”

I don’t quite understand the reasoning for dropping that second term b/c it’s “very small”

• DONE Completed: 2022-05-12

  dominated like BigO

Example: Derive volume formula for cones Find the volume of a cone w/ radius r and height h.

Bounded by x, y, and the line: $y=h-\frac{h}{r}x$.

Cylindrical shells $\begin{array}{rl}& {\int }_0^r\pi 2x[h-\frac{h}{r}x]dx\\ & ={\int }_0^{r}2xh\pi -2x^2\frac{h}{r}\pi dx\\ & =\pi h{x}^2-\frac{2}{3}{x}^3\frac{h}{r}\pi {|}_0^r\\ & =\pi h{r}^2-\frac{2}{3}{r}^3\frac{h}{r}\pi \\ & =\pi h{r}^2(1-\frac{2}{3})\\ & =\pi h{r}^2\frac{1}{3}\end{array}$

Q: I’m not clear on how some of the terms get turned from r to x but not all?

• DONE Completed: 2022-05-11

$\pi h2r(dr)$ turned into $\pi 2x[h..]dx$. How did the r turn into an x there? Why is there still an r in the height formula?

So we need to know the slope of the line to bound the cone. That slope is in terms of R, b/c the base of the cone is R wide. We can’t replace that w/ r.

cross-sectional disks

radius is a function for the line from above, but in terms of x not y. $\begin{array}{r}x=\frac{r}{h}(h-y)\end{array}$

$\begin{array}{rl}& {\int }_0^h\pi r^{2}dy\\ & {\int }_0^h\pi (\frac{r}{h}(y-h){)}^{2}dy\end{array}$ … Kinda lost track with the algebra, but it came out to the same answer.

Why did the h-y and y-h flip here?

• DONE Completed: 2022-05-08

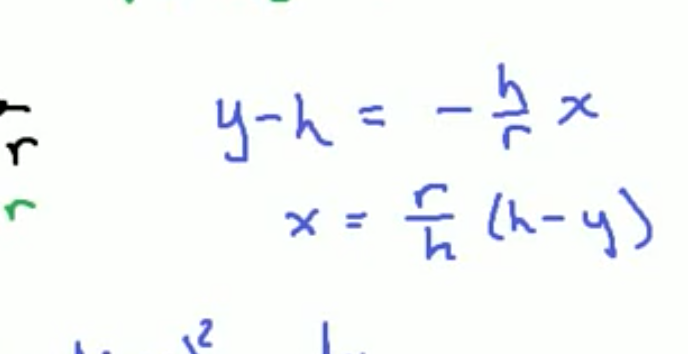
I believe it’s b/c we had to multiply both sides by $-\frac{r}{h}$ which would flip the signs there as well.

Homework

Section 7.1 (pp.359-361) -5-12, 13, 14, 15, 17,21-26

Section 7.2 (pp.368-369) -5-18, 19, 20

Section 7.3 (pp.376-377) -5-12,13-18

7.2 6

import graph;
size(400,IgnoreAspect);
real f(real x) { return 5x;}
 
fill((1,0)--(1,f(1))--(2,f(2))--(2,0)--cycle,cyan);
draw(graph(f,0,2.5),blue+1.2, "$y=5x$");
 
xaxis("$x$",BottomTop,LeftTicks);
yaxis("$y$",LeftRight,RightTicks(trailingzero));
 
label("$y=5x$",(1.2,8),black);
 
pen p = white;
shipout(bbox(p,Fill));

$\begin{array}{rlr}& {\int }_2^1\pi r^{2}dx& \\ & {\int }_2^1\pi (5x{)}^{2}dx& \\ & {\int }_2^1\pi 25x^{2}dx& \\ & {\int }_2^1\pi 25x^{2}dx& \\ & =\frac{25\pi }{3}{x}^3{|}_2^1& \\ & =\frac{25\pi }{3}-\frac{25\pi }{3}{2}^3& \\ & =\frac{25\pi }{3}-\frac{8(25\pi )}{3}& \\ & =\frac{25\pi }{3}-\frac{200\pi }{3}& \\ & =-\frac{175\pi }{3}& \\ & =\frac{175\pi }{3}& \text{absolute value as if I got the integrals in the right order}\end{array}$

7.3 6 $\begin{array}{rl}& {\int }_1^2\pi h2rdr\\ & {\int }_1^2\pi h2xdx\\ & {\int }_1^2\pi 5x2xdx\\ & {\int }_1^2\pi 10x^{2}dx\\ & =\frac{10\pi }{3}{x}^3{|}_1^2\\ & =\frac{10\pi }{3}{2}^3-\frac{10\pi }{3}\\ & =\frac{80\pi }{3}-\frac{10\pi }{3}\\ & =\frac{70\pi }{3}\end{array}$